Home

Electrolysis | Electrolytes and Non-Electrolytes

Electrolysis is the chemical change or decomposition of molten or aqueous solutions of chemical compounds at the electrodes by electric current passed into them, resulting in their conduction of electricity. Thus, electrical energy can be used to produce chemical change at the electrodes.

Chemical substances which exhibit this phenomenon are called electrolytes – some of them can conduct electricity strongly and are called strong electrolytes, while others slightly, weak electrolytes.

Strong electrolytes are substances which ionize completely in solution or in their molten state.

Examples of strong electrolytes: MgO, CuSO4, HCl and NaCl - these are ionic compounds and polar covalent compounds, such as HCl; while weak electrolytes ionize partially in solution.

Examples of weak electrolytes: ethanoic acid, CH₃COOH; ammonia, NH₃; trioxocarbonate(IV) acid; citric acid and tartaric acid - these are polar covalent compounds.

However, some chemical substances in solution do not conduct electricity at all – these are called non-electrolytes. These substances exist in molecules and are not capable of ionizng in solution.

Examples of non-electrolytes: sugar, trichloromethane, CHCl₃, ethanol, C₂H₅OH and urea (carbamide) CON₂H₄.

Faraday’s Laws of Electrolysis

Faraday’s laws of electrolysis expressed the dependence on the quantitative or measurable results of electrolysis (i.e. the amount of an element in moles liberated during electrolysis) on the following factors: 1. The time of passing the steady current (in seconds). 2. The magnitude of the steady current passed. 3. The charge on the ion of the element.

Note: quantity of electricity (coulombs) = current (amps) x time (seconds)

Q = It

To investigate factors 1 and 2 above, we have: Faraday’s first law of electrolysis:

Faraday's first law of electrolysis states that the mass of a substance liberated at (or dissolved from) an electrode during electrolysis is proportional to the quantity of electricity passing through the electrolyte.

I.e., M α Q,

M = ZQ

where M = mass of the substance liberated, Z = a constant called electrochemical equivalent of the substance, Q = quantity of electricity.

Since It = Q, then M = ZIt

By plotting the graph of mass (m) of substance deposited against the quantity of electricity applied, we have a +ve straight line graph, which passes through the origin:

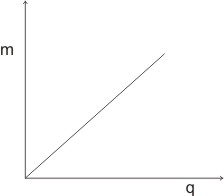
To liberate one mole of an element, the least quantity of electricity required is 96500 coulomb (1 Faraday), and this applies to an element with one positively charged ions.

Therefore, 1 Faraday will liberate 1 mole of hydrogen ions, H⁺; 1 mole of sodium ions, Na⁺ and 1 mole of silver ions, Ag⁺.

I.e. Ag⁺(aq) + e^-(aq) → Ag(s)

H⁺(aq) + e^-(aq) → ½ H₂(g)

Na⁺(aq) + e^-(aq) → Na(s)

Note: 1 Faraday is equivalent to 1 mole of elements. In general, to liberate 1 mole of ions with a charge c, the quantity of electricity that would be required is c x 1 F (i.e. 96500c Coulombs).

Example, to liberate 1 mole of copper,  Cu²⁺ + 2e^-(aq) → Cu(s)

2 x 1 F = 2 x 96500 C = 193000 C of electricity is needed.

Examples, 1. When a solution of potassium iodide was electrolyzed, 1.27 g of iodine was liberated. Calculate the number of coulombs of electricity required for the electrolysis (I = 127).

Solution: Convert mass of I₂ liberated to number of moles

I.e. Number of moles of iodine = mass (g)/Molar mass

                                            = 1.27/254 = 0.005 mole

The equation of reaction is 2I^-(aq) → I₂(g) + 2e^- (aq)

1 mole of I₂ requires 2 moles of electrons = 2 faraday to be liberated.

I.e. 1 mole of iodine gas requires 2 x 96500 C to be liberated.

Therefore, 0.005 mole required 2 x 96500 x 0.005 = 965 C to be liberated.

Note: 1 mole of iodine is expressed as two atoms, i.e. I₂ and not I. Hence, two moles of electrons are given out to liberate 1 mole of the gas as shown in the reaction equation above.

Also, since 1 mole of free iodine is expressed as I₂, its molar mass is 2 x 127 = 254 g/mole

2. During the electrolysis of a copper(II) salt, the quantity of electricity passed was 9650 coulombs. Calculate (i) the number of moles of copper metal deposited. (ii) The mass of copper deposited. (1 Faraday = 96500 coulombs, Cu = 64)

Solution: i. The equation of reaction is Cu²⁺(aq) + 2e^-(aq) → Cu(s)

2 moles of e^- are needed to deposit 1 mole of Cu(s). Therefore, 2 Faraday = 2 x 96500 C are required to deposit 1 mole of copper.

I.e. 2 x 96500 C deposits 1 mole, 9650 C will deposit

9650 / (2 x 96500) mole = 0.05 mole

ii. Converting number of moles to mass (g)

Mass (g) = number of moles x molar mass = 0.05 x 64 = 3.2 g

To investigate the dependence of the amount of element in moles liberated during electrolysis on the charge on the ion of the element, Faraday derived his second law.

Faraday’s Second Law of Electrolysis

Faraday's second law of electrolysis states that when the same quantity of electricity is passed through solutions of different electrolytes, the relative numbers of moles of the elements deposited are inversely proportional to the charge on the ions of each of the elements respectively.

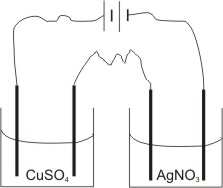
To illustrate this law, let us use a solution of copper(II) sulphate and a solution of silver trioxonitrate (V).

By passing the same quantity of electricity into the two solutions for the same length of time, it will be found that the amount of moles of silver deposited is twice that of copper deposited in the respective electrolytes.

I.e., if 0.0070 mole of silver is deposited, then 0.0035 mole of copper will be deposited. (i.e. the ratio of the number of moles of silver deposited to that of copper is 2:1, compared with the ratio of the charges on their ions, which is 1:2 respectively).

Explanation:

Calculations:

Que. If 10.8 g of silver is deposited in a cell containing AgNO₃ solution connected in series with a cell containing CuSO₄ solution, find (i). The mass of copper deposited. (ii). The total volume of oxygen liberated. (Cu=64, Ag=108, G.M.V. at s.t.p. = 22.40 dm³)

Solution

(i). Converting 10.8 g of silver to number of moles:

Number of moles = 10.8/108 = 0.1 mole of Ag is deposited.

From Faraday’s second law, the ratio of moles of Ag to Cu deposited is 2:1. Therefore, the number of moles of Cu deposited is 0.1 / 2 = 0.05 mole

Converting this to mass, Mass = number of moles x molar mass

= 0.05 x 64 = 3.2 g of copper is deposited

(ii). To determine the quantity of electricity passed: from the cathode reaction: Ag⁺(aq) + e^-(aq) → Ag(s)

1 mole of Ag is deposited by 1 F, 0.1 mole will be deposited by 0.1 F

Therefore, 0.1 F is the electricity passed into both cells. At the anode of the AgNO₃ cell: OH^- is discharged:

2OH^-(aq) → H₂O(l) + 1/2O₂(g) + 2e^-(aq)

2 F liberate 1/2 (or 0.5) mole of oxygen,

0.1 F will liberate 0.5/2  x 0.1 mole = 0.025 mole of oxygen.

At s.t.p. 1 mole of a gas occupies 22.4 dm³, therefore, 0.025 mole occupies 22.4 x 0.025 dm³ = 0.56 dm³.

At the anode of the CuSO₄ cell: OH^- is discharged:

2OH^-(aq) → H₂O(l) + 1/2O₂(g) + 2e^-(aq)

The calculation is similar to that of the AgNO₃ cell. Hence, 0.56 dm³ of oxygen is produced here also. Total volume of oxygen produced is 0.56 dm³ x 2 = 1.12 dm³.