|
Home
pH as a Scale of Acidity
The term pH denotes hydronium ion concentration in a
solution. Water undergoes slight ionization to give hydronium ion (acidic
character), and hydroxyl ion (basic character) - water is amphoteric.
|
H2O(l) |
 |
H3O+(aq) |
+ |
OH-(aq) |
Therefore, a solution would either be acidic or
basic depending on which ion is more in concentration, i.e. H3O+
or OH-. For pure water, the concentration of both ions are the same,
and each is found at 25oC to be 10-7 mol/dm3.
The equilibrium constant for the autoionization of water above is
Kw = [H3O+] [OH-]
Where Kw is the ionic product of water, [H3O+]
is the concentration of hydronium ions and [OH-] is the concentration
of hydroxyl ions. For pure water:
[H3O+] = [OH-] =10-7 mol/dm3
Therefore, Kw = 10-7 x 10-7 = 10-14
mol2 dm-6
l.e. Kw = 10-14 mol2 dm-6 at 25oC
lf however the concentration of H3O+ is more than 10-7
mol dm-3, the concentration of OH- will be less than 10-7
mol dm3, and the solution will be acidic.
In the same sense, the higher the concentration of
OH- than 10-7 mol dm3, the lower the conc. of H3O+
than 10-7 mol dm-3, and the solution will be basic.
When the conc. of both are exactly equal, the
solution will be neutral.
The dissolution of substances in water may increase
or reduce the concentrations of any of H3O+ or OH-.
lf [H3O+] is increased more than [OH-], the
solution is acidic. The solution is basic if [OH-] is greater.
The pH of a solution is defined as the negative
logarithm to base 10 of the hydronium ion concentration.
l.e. pH = - log [H3O+]
Note: the lower the numerical value of pH, the higher the concentration of H3O+
and the lower the conc. of OH- and vice versa.
It is also possible to use hydroxyl ion concentration (i.e. pOH) to indicate
alkalinity.
l.e. pOH = - log [OH-]
Since [H3O+] [OH-] = 10-14
pH + pOH = 14
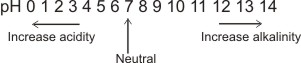
The pH scale
pH Calculations
1. Calculate the pH of a solution, which has hydronium ion concentration of
6.0 x10-5 M
Solution
pH = -log [6.0 x10-5]
pH = - [log 6.0 + log10-5]
pH = - [0.78 - 5] = 4.22
(2). Calculate the hydronium ion concentration of a solution which has a pH of
11.73
Solution
pH = - log [H3O+]
11.73 = - log [H3O+]
log [H3O+] = - 11.73
[H3O+] = antilog of - 11.73
To obtain the antilog of - 11.73 from the anti-logarithm table, - 11.73 must be
expanded into a positive and a negative number. The negative part should be an
whole number, while the positive number a fraction.
To obtain these two numbers, break
-11.75 into -11 and -0.73. Then, you can subtract 1 from -11 and balance up by
adding 1 to -0.73.
i.e. -11 - 1 = -12 and -0.73 + 1 = 0.27.
Therefore, -11.73 = - 12 + 0.27
From the antilog table, antilog of -12 is 10-12, antilog of 0.27 is
1.9.
Therefore [H3O+] = 1.9 x10-12 M
|