|
Home
What is Solubility Product?
The concept of solubility product arises when an ionic solid is dissolved in water
with its ions becoming the actual solutes.
Example, when solid silver chloride, AgCl is shaken with water, the following equation is obtained for its saturated solution:
| AgCl(s) |
 |
Ag+(aq) |
+ |
Cl-(aq) |
The concentrations of the ions, Ag+ and Cl- in solution depends on the solubility of AgCl. The above equation is reversible, indicating AgCl to be slightly soluble in water. Hence, an equilibrium constant, similar to that of any chemical equilibrium can be written as thus:
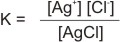 |
since AgCl is pure solid (slightly soluble), its
concentration is taken as constant. |
Therefore:
K = Ksp = [Ag+] [Cl-]
Where Ksp is called the solubility product constant, [Ag+] is conc. of silver ions in moles per dm3, [Cl-] is conc. of chloride ions in moles per dm3
Note:
- The constant Ksp applies to the process in which the forward reaction is the dissolving of an insoluble or slightly soluble ionic substance in water.
- If the ions have unequal number of cations and anions, the Ksp expression is written, such that the coefficients of the ions in the balanced chemical equation become the exponents of the respective concentration term in the Ksp expression. Example, the expression for the reaction:
| Mg(OH)2(s) |
 |
Mg2+(aq) |
+ |
2OH-(aq) |
Ksp = [Mg2+] [OH-]2
- Generally, solubility product refers only to insoluble or slightly soluble ionic substances in water (these produce ionic equilibria in solution). It is the product of the concentrations of the ions raised to the coefficients of their respective ion.
- If the molar concentrations of the ions of a slightly soluble substance are known, the numerical value of Ksp can be found. Conversely, if Ksp is known, the concentration of the ions in equilibrium with the undissolved can be determined.
Simple Calculations on
Solubility Product
1. When a sample of solid AgCl is shaken with water at 25oC, 1.0 x 1.0-5 M silver ion is produced, calculation the Ksp.
Solution:
| AgCl(s) |
 |
Ag+(aq) |
+ |
Cl-(aq) |
Ksp = [Ag+] [Cl-]
From the stoichiometry of reaction, mole ratio of Ag+ to Cl- is 1:1
Therefore, [Ag+] = [Cl-] = 1.0 x 10-5 M
Ksp = (1.0 x 10-5) (1.0 x 10-5)
= 1.0 x 10-10 M2 (mol2 dm-6)
2. Calculate the solubility of Mg(OH)2 in water Ksp = 1.2 x 10-11 mol3 dm-9
Solution:
| Mg(OH)2(s) |
 |
Mg2+(aq) |
+ |
2OH-(aq) |
From the stoichiometry, mole ratio of Mg2+ to OH- is 1:2
Ksp = [Mg2+] [OH-]2
Let [Mg2+] = X, therefore [OH-] = 2X (mole ratio is 1:2).
Hence, Ksp = X (2X)2 = 1.2 x 10-11
4X3 = 12 x 10-12
X3 = 3 x 10–12
| X |
= |
 |
X = 1.4 x 10-4 M = conc. of Mg2+ ions.
From the stoichiometry:
1 mole of Mg(OH)2 dissolves to produce 1 mole of Mg2+ ions and 2 moles of OH- ions. Therefore,
1.4 x 10-4 mole of Mg(OH)2 dissolved to produce 1.4 x10-4 mole of Mg2+ ions and
2.8 x 10-4 mole of OH- ions.
Hence, for 1 dm3 of solution, the solubility of Mg(OH)2 is 1.4 x 10-4 M
|